Dr. B. Fiedler:
 
VL Schnelle diskrete Fouriertransformationen

Termin:

• Do, 11:15-12:45, Seminargebäude 3-03

Teilnehmerkreis:

• Studenten der Mathematik, Physik und Informatik, höhere Semester
• Studenten des Graduiertenstudiums

Inhaltliche Schwerpunkte:

Diskrete Fouriertransformationen sind Isomorphismenvon Gruppenringenendlicher Gruppen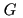auf Ringe, die äußere direkte Produkte voller Matrixringesind (Blockdiagonalmatrizen). Ihre Existenz stellt der Satz von Wedderburn sicher.

Bei großen Gruppen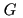führen computeralgebraische Rechnungen inoft zu einem hohen Bedarf an Zeit und Memory oder sind gar nicht mehr ausführbar, während das Rechnen mit den Blockdiagonalmatrizen ausoft noch möglich ist. Diskrete Fouriertransformationensind somit wichtige Hilfsmittel für Computerrechnungen in.

Die Konstruktion diskreter Fouriertransformationen beruht auf der Darstellungstheorie endlicher Gruppen, die hier umfassend Anwendung findet. Für wichtige Klassen endlicher Gruppen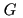kennt man sogar schnelle Berechnungsalgorithmen für. Neben der Konstruktion werden auch Anwendungen diskreter Fouriertransformationen behandelt. Ferner sind Beispielrechnungen mit Mathematica geplant. Einige Schwerpunkte sind:

• Grundlagen aus der Darstellungstheorie und Theorie der Gruppenringe endlicher Gruppen
• Konstruktionen von diskreten Fouriertransformationen (abelsche, auflösbare, überauflösbare Gruppen; Symmetrieanpassung)
• Darstellungstheorie symmetrischer Gruppen
• Diskrete Fouriertransformationen symmetrischer Gruppen
• Anwendungen (Zirkulant-Matrizen, effizientes Rechnen, Filtering, Irrfahrten, Codes, Learning)

Literatur:

1. Clausen, M., Baum, U.: Fast Fourier Transforms. Mannheim, Leipzig, Wien, Zürich: BI Wissenschaftsverlag, 1993.
2. Boerner, H.: Darstellungen von Gruppen. Berlin, Göttingen, Heidelberg: Springer-Verlag, 1955.
3. Boerner, H.: Representations of Groups (2. Ed.). Amsterdam: North-Holland Publishing Company, 1970.
4. Serre, J. P.: Lineare Darstellungen endlicher Gruppen. Braunschweig: Friedr. Vieweg + Sohn, 1972.
5. James, G. D., Kerber, A.: The Representation Theory of Symmetric Groups. Addison-Wesley, 1981
6. Kerber, A.: Representations of Permutation Groups (Lecture Notes in Mathematics: Vol. 240). Berlin, Heidelberg, New York: Springer-Verlag 1971.

Erwartete Vorkenntnisse:

Grundwissen zur Darstellungstheorie und Gruppentheorie

Scheinvergabe:

Es wird ein Teilnahmeschein vergeben.